1.フィルターによる音声信号処理の仕組み
(1)フィルター係数の取得処理
フィルター係数の取得処理(フィルター係数の計算)は、それが必要になった時点で1回だけ行います。いったん取得したフィルター係数は、音声信号処理で繰り返し使用されます。
FIRフィルターのフィルター係数は、目的の周波数特性を逆フーリエ変換することによって\(b(m)\)の形で求めることができました。これは以下に示すように、前章の「ローパスフィルターの設計」式(3-3~5)で述べたsinc関数です。
\[
b(m) = 2f_e sinc (2{\pi}f_em) \, \,({-\infty} \le m \le {\infty})\tag{3-3}
\]
ただし\(sinc(x)\)はシンク関数で次の性質を持っています。
\[
sinc(x) = \begin{cases}
1 \, \,\,\, (x = 0) \\
\cfrac{\sin(x)}{x} \, \, (otherwise)
\end{cases}\tag{3-4}
\]
したがって、(\(x \ne 0\))における最終的なフィルター係数\(b(m)\)は次のようになります。\[
b(m) = 2f_e \cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em} \, \,({-\infty} \le m\le{\infty})\tag{3-5}
\]
これからわかるように、\(x=0\)の時に\(b(m)\)は最大値をとり、それ以外では対称となります(前章のグラフ「理想的なローパスフィルターの逆フーリエ変換結果」で見たとおり)。そこで、フィルター係数も対称になるように工夫すると考えやすくなります。
前章の図「FIRデジタルフィルターの構成」で、遅延器の数\(J\)に対してフィルター係数の数は\(J+1\)になることを説明しましたが、ここで、この\(J\)を「フィルター次数N」と呼ぶことにしましょう。そして、フィルター係数を格納する実数配列をhで表すことにします。最大値を中心に対称になる特性を考えると、Nを偶数にして、hの配列サイズをN+1にすれば扱いやすいことがわかります。
この前提に立つと、上式\((3-5)\)は\(m\)を\((-N/2\le m\le N/2)\)の範囲で求めればよいことになります。さらに窓関数\(w(x)\)を掛けるので、ローパスフィルターのフィルター係数計算式は次のように書き換えてプログラミングすることにします。
\[
h\Biggl[\cfrac{N}{2}+m\Biggr] = 2f_e\cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em}{w(m)} \, \,\Biggl(-\cfrac{N}{2}\le m\le\cfrac{N}{2}\Biggr)
\]
ここで求められたフィルター係数は窓関数が適用されているので、そのまま音声信号処理で使用することができます。
(2)フィルター係数による音声信号処理
入力された音声信号にフィルター係数を適用して、目的とする周波数領域の遮断または通過処理を行います。継続的に大量の計算が発生する処理です。理論的にはフィルター次数を大きくするほど高性能になります。しかし次数を高くしすぎると、計算処理による遅延が発生します。一方で次数が低すぎるとフィルタリングの性能は低下します。満足できる性能が得られるなら、次数は低いほど良いとされています。
どの程度の次数が適切かは、試行によって決めることになりそうです。
2.対象フィルターとデータ型の検討
前章では4種類のフィルターを設計しましたが、用途から判断してバンドエリミネータを除く3種類のフィルターを作成することにします。先ほどプログラミング用に改変した式の例に沿って、これらの計算式を整理しておきましょう。
①ローパスフィルター
\[
h\Biggl[\cfrac{N}{2}+m\Biggr] = 2f_e \cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em}{w(m)} \, \,\Biggl(-\cfrac{N}{2}\le m\le\cfrac{N}{2}\Biggr)\tag{1}
\]
②ハイパスフィルター
\[
h\Biggl[\cfrac{N}{2}+m\Biggr] = \Biggl(\cfrac{sin(2{\pi}m)}{2{\pi}m} - 2f_e \cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em}\Biggr){w(m)} \, \,\Biggl(-\cfrac{N}{2}\le m\le\cfrac{N}{2}\Biggr)\tag{2}
\]
③バンドパスフィルター
\[
h\Biggl[\cfrac{N}{2}+m\Biggr] = \Biggl(2f_{e2}\cfrac{sin(2{\pi}f_{e2}m)}{2{\pi}f_{e2}m} - 2f_{e1}\cfrac{\sin(2{\pi}f_{e1}m)}{2{\pi}f_{e1}m}\Biggr){w(m)} \, \,\Biggl(-\cfrac{N}{2}\le m\le\cfrac{N}{2}\Biggr)\tag{3}
\]
○ハニング窓関数
上記の各式の\(w(m)\)は次のとおりです。
\[
w(m) = 0.5 \Biggl(1 - \cos 2{\pi}\Biggl(\cfrac{N}{2}+m\Biggr)\Biggr)\tag{4}
\]
(1)データ型の検討
FIRフィルターを実現するには膨大な計算量が発生します。係数を計算する部分は係数が必要になった時に1度実行するだけなので問題ありませんが、係数を適用する信号処理の部分は連続動作するので速度には敏感になってしまいます。実数形式を扱うため、C言語のデータ型としては単精度浮動小数点型(float:4バイト、有効桁数7桁)か倍精度浮動小数点型(double:8バイト、有効桁数16桁)を選択することになります。速度だけでなくデータの精度も重要なので、Raspberry Pi Zeroがどの程度の計算能力を持っているかを計測することにしました。
次のようにdoubleとfloatを定義して、片方の組だけを使って信号処理に似た乗算と加算の組み合わせを1億回計算させてみます。
| double dt = 0.0; double a = 1.2345678901234; double b = 0.9876543210234; /* float dt = 0.0; float a = 1.2345678901234; float b = 0.9876543210234; */ |
| long limit = 100000000; for (long i=0; i&tl limit; i++) dt = dt + a * b; |
・float: 3.876473秒
・double: 3.983663秒
その差は1億回の計算でわずか0.107190秒とほぼ無視できるので、double型を採用することにします。
(2)変数定義と関数の名称・形式
関数の引数で使用するデータは以下のとおりです。先に述たように、計算結果のフィルター係数はフィルターの次数Nより1つ大きいサイズの数値配列に格納します。したがって、この配列は次のように定義することになります。
double h[N+1];
Nは下にあるようにフィルターの次数で、必ず偶数の値を指定します。関数には配列hへのポインターを渡します。
| double fe | : | 遮断周波数(Hz) | |
| double fe1 | : | 低域遮断周波数(Hz) | |
| double fe2 | : | 高域遮断周波数(Hz) | |
| double fs | : | サンプリング周波数(Hz) | |
| int N | : | フィルターの次数 | |
| double* h | : | フィルター係数配列 |
| ローパスフィルター | : | void getCoefficientLPF(double fe, double fs, int N, double* h); | |
| ハイパスフィルター | : | void getCoefficientHPF(double fe, double fs, int N, double* h); | |
| バンドパスフィルター | : | void getCoefficientBPF(double fe1, double fe2, double fs, int N, double* h); |
3.フィルター係数取得関数の作成
3種類のフィルターは、すべて次のフローチャートに沿ってC言語で記述します。
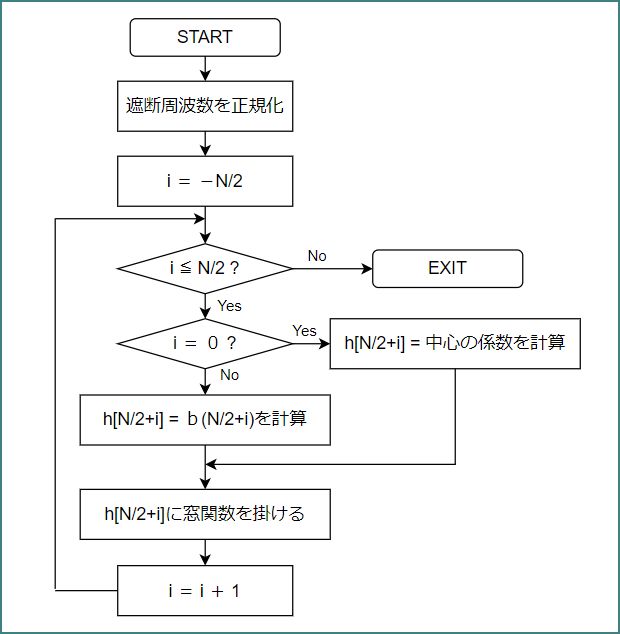
ここでは、ローパスフィルターのコードを例示します。全体のコードファイルfilter.cやヘッダーファイルfilter.hは、後述のテストプログラム共々、冒頭に配置した[Download]ボタンでダウンロードしてください。

| #include <math.h> #include "filter.h" /* getCoefficientLPF : ローパスフィルターの係数を求める [引数] double fe : 遮断周波数 double fs : サンプリング周波数 int N : フィルターの次数 double* h : フィルター係数配列 */ void getCoefficientLPF(double fe, double fs, int N, double* h) { fe = fe / fs; // 遮断周波数を正規化する for (int i=-N/2; i<=N/2; i++) { if (i == 0) h[N/2+i] = 2.0 * fe; // 中心のフィルター係数は1 else { h[N/2+i] = 2.0 * fe * sin(2.0 * M_PI * fe * i) // フィルター係数の計算 / (2.0 * M_PI * fe * i); } // 窓関数をかける h[N/2+i] = h[N/2+i] * 0.5 * (1.0 - cos(2.0 * M_PI * (N/2+i) / N)); } } |
4.フィルター係数の検証
フィルター係数取得関数をテストするために、次の簡単なプログラムtestFilterCoef.cを書きました。
#include <stdio.h>
#include "filter.h"
#define SAMPLE_RATE (16000)
int main(void){
int N=64; // フィルタ次数
double h[64+1] = {0}; // フィルタ係数
double fe; // 遮断周波数
double fe1, fe2; // 遮断周波数低域,高域
fe = 1000.0; // 遮断周波数[Hz]
getCoefficientLPF(fe, SAMPLE_RATE, N, h);
printf("\n[Low-Pass Filter]\n");
for (int i=-N/2; i<=N/2; i++)
printf("%+3d : %+1.15e\n", i, h[N/2+i]);
fe = 3000.0; // 遮断周波数[Hz]
getCoefficientHPF(fe, SAMPLE_RATE, N, h);
printf("\n[High-Pass Filter]\n");
for (int i=-N/2; i<=N/2; i++)
printf("%+3d : %+1.15e\n", i, h[N/2+i]);
fe1 = 2000.0; // 低域遮断周波数[Hz]
fe2 = 4000.0; // 高域遮断周波数[Hz]
getCoefficientBPF(fe1, fe2, SAMPLE_RATE, N, h);
printf("\n[Band-Pass Filter]\n");
for (int i=-N/2; i<=N/2; i++)
printf("%+3d : %+1.15e\n", i, h[N/2+i]);
}
まず以下のようにfilter.cをコンパイルしてください。オプションパラメータの-cは、コンパイルだけしてリンクはしない指示です。同名のオブジェクトファイルfilter.oが作成されます。
続いてtestFilterCoef.cをコンパイルします。オプションパラメータの-oで出力ファイル名を指定、testFilterCoef.cのコンパイル結果とfilter.o、それに-lmでmathライブラリーをリンクするよう指定しています。
そしてtestFilterCoefを実行してください。
| $ gcc -c filter.c |
| $ gcc -o testFilterCoef testFilterCoef.c filter.o -lm |
| $ ./testFilterCoef [Low-Pass Filter] -32 : -0.000000000000000e+00 -31 : -9.460607877808004e-06 -30 : -7.208052318064732e-05 -29 : -2.183273377134122e-04 -28 : -4.326767382605224e-04 -27 : -6.430480233855353e-04 -26 : -7.294743164052953e-04 -25 : -5.530006490108483e-04 -24 : +7.135925596965839e-19 -23 : +9.681577380000450e-04 -22 : +2.273450969308825e-03 -21 : +3.701229565134124e-03 -20 : +4.912449159580915e-03 -19 : +5.492449320879931e-03 -18 : +5.032453584178068e-03 -17 : +3.231537169519118e-03 -16 : -2.436357395324609e-18 -15 : -4.458385861248614e-03 -14 : -9.606779608862236e-03 -13 : -1.459411167265251e-02 -12 : -1.833840858268103e-02 -11 : -1.966856072485316e-02 -10 : -1.750631577144824e-02 -9 : -1.106047686961701e-02 -8 : +4.159122230952635e-18 -7 : +1.542670051075470e-02 -6 : +3.435212446878982e-02 -5 : +5.534353844195839e-02 -4 : +7.654873437812401e-02 -3 : +9.591616534917083e-02 -2 : +1.114583316719285e-01 -1 : +1.215186409563420e-01 +0 : +1.250000000000000e-01 +1 : +1.215186409563420e-01 +2 : +1.114583316719285e-01 +3 : +9.591616534917084e-02 +4 : +7.654873437812403e-02 +5 : +5.534353844195839e-02 +6 : +3.435212446878982e-02 +7 : +1.542670051075470e-02 +8 : +4.159122230952636e-18 +9 : -1.106047686961701e-02 +10 : -1.750631577144824e-02 : (以下省略) : |
実行と同時に3種類のフィルター係数が表示されます。ここでは[Low-Pass Filter]の一部を掲げていますが、
中央の「 +0 : +1.250000000000000e-01」を境界に対称的に値が並んでいるのがわかります。
この値を検証するために、たいへん便利なサイトを見つけました。と言うより、そこは様々なフィルターを設計できる素晴らしいサイトです。まずは次のリンクをクリックして、「FIRフィルタ設計・窓関数法」を選択してください。
石川高専 山田洋士研究室『Digital Filter Design Services』
同じ条件で計算させるために、フィルター長に「フィルター次数+1」の65、フィルターの種別はLPF、窓の種類は「Hann窓」を選んで、正規化遮断周波数には0.0625を指定(遮断周波数をサンプリング周波数で正規化 = 1000 / 16000)して[設計する]ボタンをクリックします。
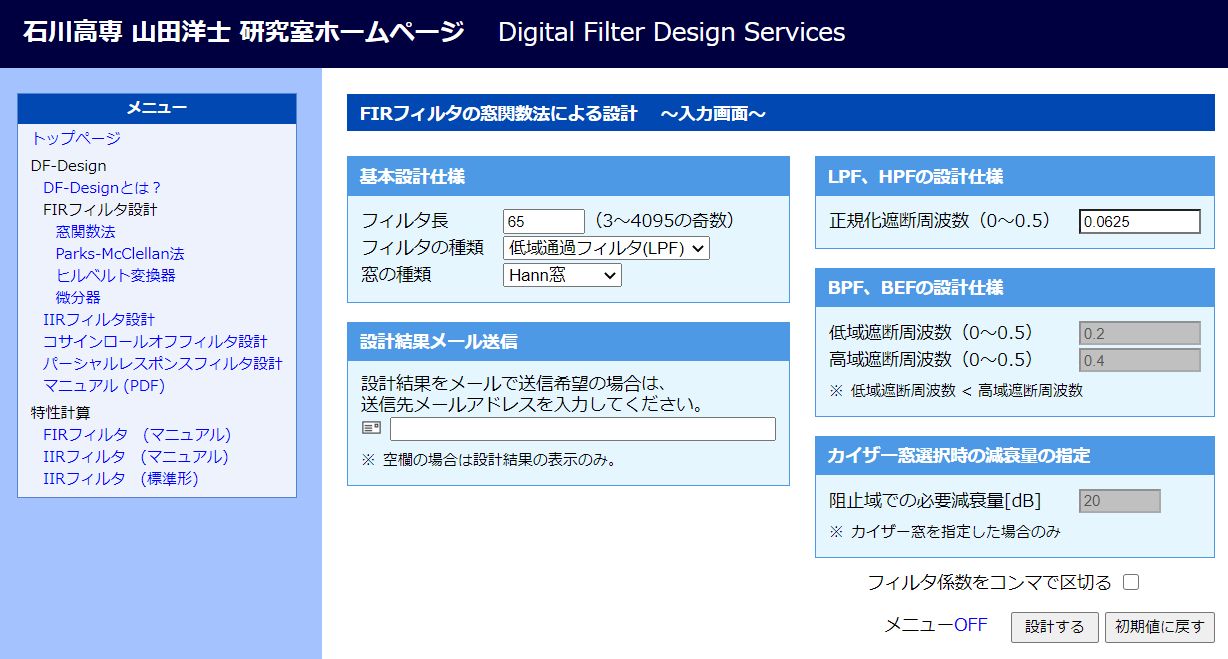
すると次のような計算結果が表示されます。
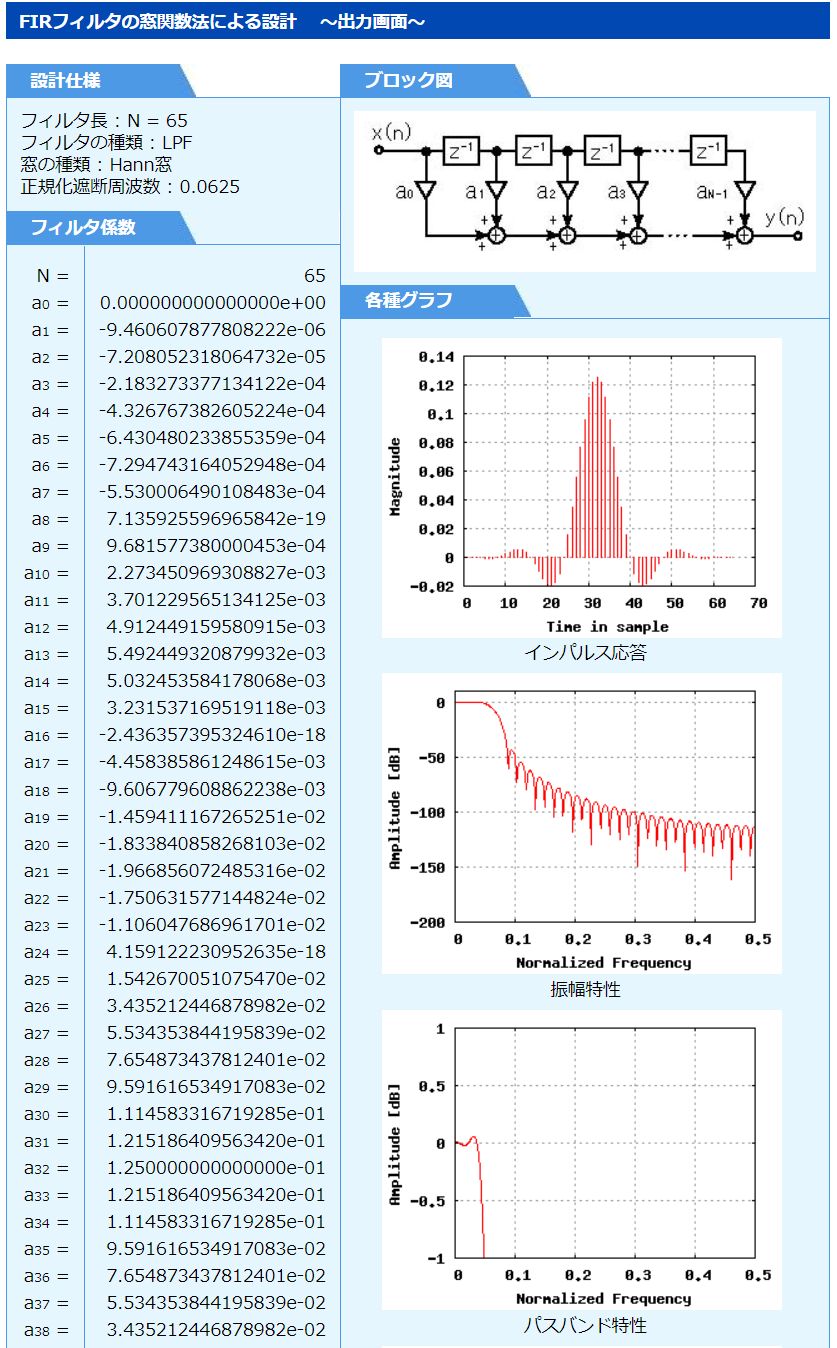
表示されたフィルター係数と、先に取得した[Low-Pass Filter]の係数とを比べてみましょう。一部でわずかな違い(仮数部の少数以下14桁より小さい部分で)はありますが、ほぼ同じ値になっています。同様にして比較するとバンドパスフィルターでも同様なのですが、ハイパスフィルターでは8ステップおきに仮数部の値に大きな違いが発生しています。その原因は計算誤差によるものと思われます。これらの値は指数部が-17~-18ときわめて微小である(どちらもゼロと見なしてかまわない)ことから、実質的な差異は無視できます。
〔ヒント〕
ここまで、音声処理の理論を垣間見ながらたどり着いたフィルター係数取得関数ですが、フィルター係数はこのサイトを利用するだけで簡単に入手できるわけです。デジタルフィルターの作成に必要なのはフィルター係数なので、必要とするフィルターの要件を指示して係数を入手できれば、それを取り込むだけで以降の音声信号処理はできるわけです。
これから向かおうとしている方向は、先に作成したフィルター取得関数を組み込んで、関数パラメータを変更することで弾力的に対応できるシステムの構築です。しかしながら、窓関数の種類を変更したり、IIRなど別の方式のフィルターを試す場合には、『Digital Filter Design Services』の力を借りるのも一法であることを押さえておきましょう。取り組みの幅が大きく広がりますし、その時、今までの知識は役立つはずです。
5.音声信号処理関数の作成
音声信号処理のロジックは実に簡単です。前章の「3.FIRフィルターの理論と特徴」の末尾で得た、「入力信号の周波数特性とフィルター係数の周波数特性をかけ合わせたものが出力信号になる」という論理に沿ってコードを記述します。
(1)変数定義と関数の名称・形式
音声信号処理関数で使用するデータは以下のとおりです。
| int order | : | フィルター次数 | |
| int frames | : | バッファのフレーム数 | |
| float *inptr | : | 入力バッファへのポインター | |
| double *h | : | フィルター係数配列へのポインター | |
| float *outptr | : | 出力バッファへのポインター |
void applyPassFilter(int order, int frames, float* inptr, double* h, float* outptr);
フィルター係数は目的に応じてローパス、ハイパス、バンドパスを指定して取得しましたが、これらはいずれもひとつのフィルター係数配列に格納されます。音声信号処理はそのフィルター係数配列を使って処理するので、いずれの場合もこの関数を呼ぶことで処理されます。
これらの変数と関数プロトタイプは、ヘッダーファイル「filter.h」に記述しています。
(2)音声信号処理関数のコードと使い方
音声信号処理関数applyPassFilterを呼ぶ前に、次のことを行っておくことが必要です。
・目的のフィルター係数を取得していること
・入力バッファと出力バッファを確保していること
・PortAudioの流儀にしたがって、初期化処理と音声信号データの入出力準備が完了していること。
これらの条件が整っている状態で、入力バッファsampleBlockに入力された音声データと共に、音声信号処理関数を呼び出して処理します。
applyPassFilter(FILTER_ORDER, FRAMES_PER_BUFFER, (float*)sampleBlock, h, (float*)buffer);
ここで、hはフィルター係数配列、bufferは変換結果の出力バッファーです。この内容をPortAudioの出力ストリームに書き出します。第1、第2引数の意味は以下のとおりです。
・FILTER_ORDER : フィルター次数
・FRAMES_PER_BUFFER : バッファのフレーム数
いずれも#define文で値が定義されています。
音声処理実行関数のコードは次のとおりです。このコードは「デジタルフィルター係数計算・音声信号処理関数」プログラムfilter.cに記述しています。
| #include <math.h> #include "filter.h" /* applyPassFilter : ロー、ハイ、バンドパス・フィルター適用処理 [引数] int order : フィルターの次数 int frames : バッファのフレーム数 float *inptr : 入力バッファへのポインター double *h : フィルター係数配列へのポインター float *outptr : 出力バッファへのポインター */ void applyPassFilter(int order, int frames, float *inptr, double *h, float *outptr) { double sl, sr, yl, yr; for (int i=0; i<frames; i++) { sl = (double)*inptr++; sr = (double)*inptr++; yl = yr = 0; for (int j=0; j<=order; j++) { yl = yl + sl * h[j]; yr = yr + sr * h[j]; } *outptr++ = (float)yl; *outptr++ = (float)yr; } } |
(3)フィルターなし信号処理の追加
今までhtskelton.cなどに記述していた「フィルターなしのフィルター適用関数 applyPassThroughFilter」の形を少し変えて、applyThroughFilterとしてfilter.cに追加することにします。新たなコードは次のとおりです。
| /* applyThroughFilter : フィルターなし(素通し)適用処理 [引数] int frames : バッファのフレーム数 float* ptr : 入力バッファへのポインター float outptr : 出力バッファへ配列 */ void applyThroughFilter(int frames, float *inptr, float *outptr) { float sl, sr; for (int i=0; i<frames; i++) { sl = *inptr++; sr = *inptr++; *outptr++ = sl; *outptr++ = sr; } } |
以上と合わせて、今後のフィルター処理のために、次のような処理モードをfilter.hに設定しておきましょう。文字キーの[b]を押すとバンドパスフィルターで動作し、[x]を押すとフィルターなしで動作するといった使い方を想定しています。
| #define MODE_LOWPASS 'l' // ローパス #define MODE_HIGHPASS 'h' // ハイパス #define MODE_BANDPASS 'b' // バンドパス #define MODE_THROUGH 'x' // フィルターなし |
これで、フィルターなしと3種類のフィルターを使用するための関数セットが出来上がりました。次回は、htskelton2.cからこれらのフィルターを自由に選択して音声信号処理できる、新たなプログラムを作成します。 お楽しみに!