１．前提事項など

①フィルターの周波数特性グラフ

　この章に掲載する周波数特性グラフは、特に断りがないものはScilabで解析して描いています。

　Scilab（サイラボ）は、1990年からフランスのINRIA（Institut National de Recherche en Informatique et en Automatique：国立情報学自動制御研究所）とENPC（École nationale des ponts et chaussées：国立土木学校）で開発されているオープンソースの数値計算システムです。数値計算機能以外に、信号処理、行列や多項式の数式処理、 関数のグラフィック表示なども充実しています。
　ダウンロードと使用方法については『Scilabのインストールと実行』などに詳しいので参照してください。
　また「オールパス・フィルター」と「ノッチ・フィルター／逆ノッチ・フィルター」の周波数特性は、Scilab用に記述されたSHINNGOUSHORIサイトのM.Tsutsuiさんのソースコードを利用させていただきました。

②フィルターのブロック図

　デジタルフィルターは、「乗算器」「加算器」「遅延器」という3種類の要素から構成されていること、およびフィルターの仕組みを表すブロック図については19章『デジタルフィルターの理論と設計』で述べたとおりですが、ここでも次の記号を使用します。

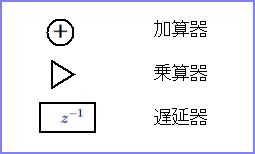
③参考文献

　・雑誌インターフェイス『音声信号処理』2016年6月号　CQ出版社(刊)
　・Yosuke Sugiura, Arata Kawamura, Youji Iiguni
　　　Graduate School of Engineering Science, Osaka University
　　　"Performance Analysis of an Inverse Notch Filter and Its Application to \(F_0\) Estimation"
　　　Scientific Research; December 29, 2012

２．オールパス・フィルター

　オールパス・フィルターは、入力した音声信号の周波数成分をすべてそのまま通します。音声信号をオールパス・フィルターに通しても聴感上の変化はありません。それだけでは何の役にも立たないのですが、特定の周波数の位相を反転させることができるという面白い特性をもっています。

(1)ブロック図

　ここで、フィルター係数は\(r\)と\(a\)です。位相反転したい周波数を\({\omega}_N\)とすると、\(a\)は次のようになります。
　　　　\(a=-(1+r)cos\ {\omega}_N\)
　\(r\)は位相特性の急峻さを決定します。\(r\)が\(0\)に近いと緩やかな特性となり、\({\omega}_N\)周辺の周波数も位相が大きく変化します。一方、\(r\)を\(1\)に近づけると急峻な特性となり、\({\omega}_N\)付近の周波数は位相がほとんど変化しなくなります。ただ後者の場合は、出力が安定するまでに時間がかかります。

(2)C言語コード

　以下にC言語でのコードを示します。位相反転周波数は1kHz、rは0.8に設定しています。マイクなどからDATA_SIZE分の音声信号を連続入力して、DATA_SIZE分ずつ音声信号処理して出力する構成です。オールパスの出力はxとして計算しています。

// 変数の準備 #define DATA_SIZE 100; double s[DATA_SIZE+1] = {0}; // 入力データ配列 double y[DATA_SIZE+1] = {0}; // 出力データ配列 double fs = 16000; // サンプリング周波数 double r = 0.8; // r値 double x, u0, u1, u2; double fc = 1000 / fs; // 位相反転周波数 double a = -(1+r) * cos(2.0*M_PI*fc); // フィルター係数 // 集音再生処理 while (1) { // y[]への出力とs[]からの音声データ入力処理 ： ： // 音声信号処理 for (int i=0; i<DATA_SIZE; i++) { u0 = s[i] - a * u1 - r * u2; // 内部信号生成 x = r * u0 + a * u1 + u2; // オールパス・フィルター出力 y[i] = x; // オールパスの結果を出力データ配列へ u2 = u1; // 信号遅延 u1 = u0; // 信号遅延 } }

(3)周波数特性

　1kHzの正弦波を入力した時のオールパス・フィルターの出力波をプロットしています。上のグラフは\(\ r=0.2\)、下は\(r=0.8\)での状態です。

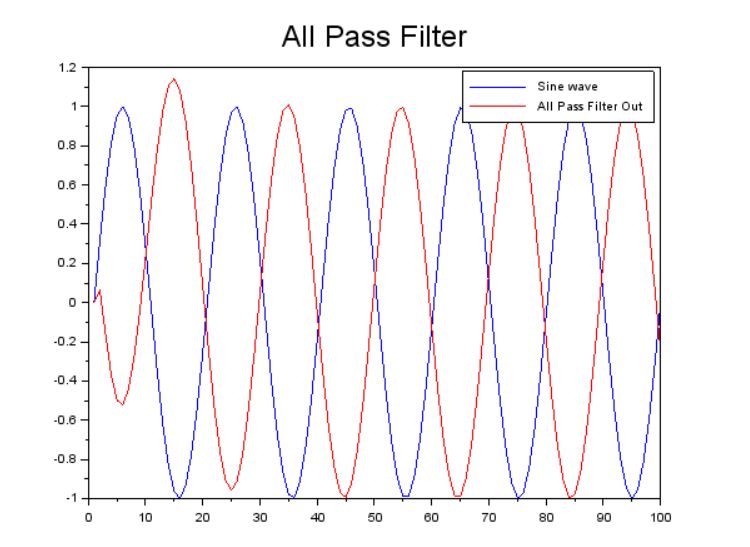
　このように、特定の周波数の位相だけを反転できる特性を利用して、特定周波数をカットするノッチ・フィルターに応用されています。なお、オールパス・フィルターについては伝達関数やインパルス応答など検討すべき事項が多いのですが、そこまで踏み込む時間と体力が不足していてすべてパス、割愛します。

３．ノッチ・フィルター

　ノッチ・フィルターは、入力音声信号に含まれる周波数成分のうち、特定の周波数だけをカットするフィルターです。

(1)ブロック図

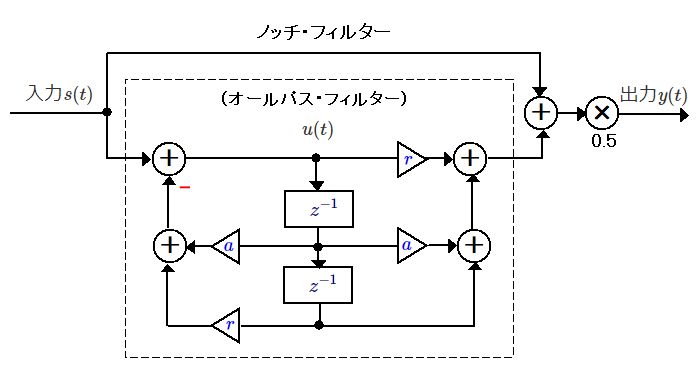
　ノッチ・フィルターのブロック図を以下に示します。破線で囲んだ部分はオールパス・フィルターです。
　オールパス・フィルターはすべての周波数を同じ大きさで通過させます。しかし、先に述べたように特定の周波数の位相を反転させることができます。そこで、入力信号とオールパス・フィルターの出力を加算すると、反転された周波数成分が相殺されて消え、残りの周波数成分の大きさは2倍になります。最後に信号を0.5倍して大きさを整えています。

(2)C言語コード

　以下にC言語によるコードを示します。遮断周波数は3kHz、rは0.8に設定しています。入力信号s[･]とオールパス・フィルターの出力xを加算して1/2したものがノッチ・フィルターの出力です。

// 変数の準備 #define DATA_SIZE 100; double s[DATA_SIZE+1] = {0}; // 入力データ配列 double y[DATA_SIZE+1] = {0}; // 出力データ配列 double fs = 16000; // サンプリング周波数 double r = 0.8; // r値 double x, u0, u1, u2; double fc = 3000 / fs; // 遮断周波数 double a = -(1+r) * cos(2.0*M_PI*fc); // フィルター係数 // 集音再生処理 while (1) { // y[]への出力とs[]からの音声データ入力処理 ： ： // 音声信号処理 for (int i=0; i<DATA_SIZE; i++) { u0 = s[i] - a * u1 - r * u2; // 内部信号生成 x = r * u0 + a * u1 + u2; // オールパス・フィルター出力 y[i] = (s[i] + x) / 2.0; // ノッチフィルターの出力を出力データ配列へ u2 = u1; // 信号遅延 u1 = u0; // 信号遅延 } }

(3)周波数特性

　遮断周波数：3kHz、r：0.8でのノッチ・フィルター周波数特性です。\(r\)は1未満の値を設定します。1に近いほど周波数特性は急峻になり、0に近いと緩やかになります。

４．逆ノッチ・フィルター

　逆ノッチ・フィルターは、入力音声信号に含まれる周波数成分のうち、特定の周波数だけを抽出するフィルターです。

(1)ブロック図

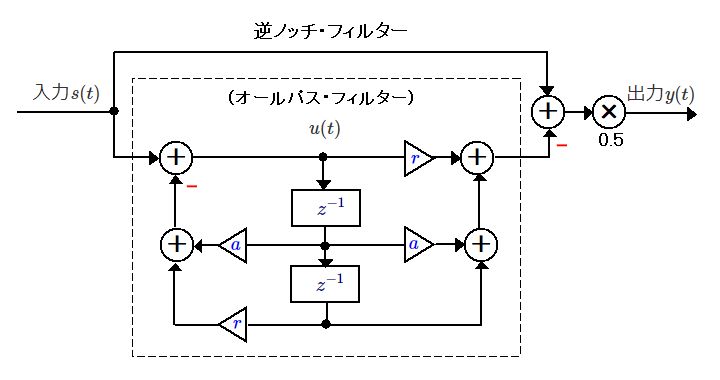
　逆ノッチ・フィルターのブロック図を以下に示します。破線で囲んだ部分はオールパス・フィルターです。
　逆ノッチ・フィルターはノッチ・フィルターの逆特性を利用するものです。オールパス・フィルターの出力を入力から減算することで実現します。ほとんどの周波数は除去され、オールパス・フィルターで反転した周波数部分が2倍になります。最後に信号を0.5倍して大きさを整えています。

(2)C言語コード

　以下にC言語でのコードを示します。抽出周波数は5kHz、rは0.8に設定しています。入力信号s[･]からオールパス・フィルターの出力xを減算して1/2したものが逆ノッチ・フィルターの出力です。

// 変数の準備 #define DATA_SIZE 100; double s[DATA_SIZE+1] = {0}; // 入力データ配列 double y[DATA_SIZE+1] = {0}; // 出力データ配列 double fs = 16000; // サンプリング周波数 double r = 0.8; // r値 double x, u0, u1, u2; double fc = 5000 / fs; // 抽出周波数 double a = -(1+r) * cos(2.0*M_PI*fc); // フィルター係数 // 集音再生処理 while (1) { // y[]への出力とs[]からの音声データ入力処理 ： ： // 音声信号処理 for (int i=0; i<DATA_SIZE; i++) { u0 = s[i] - a * u1 - r * u2; // 内部信号生成 x = r * u0 + a * u1 + u2; // オールパス・フィルター出力 y[i] = (s[i] - x) / 2.0; // 逆ノッチフィルターの出力を出力データ配列へ u2 = u1; // 信号遅延 u1 = u0; // 信号遅延 } }

(3)周波数特性

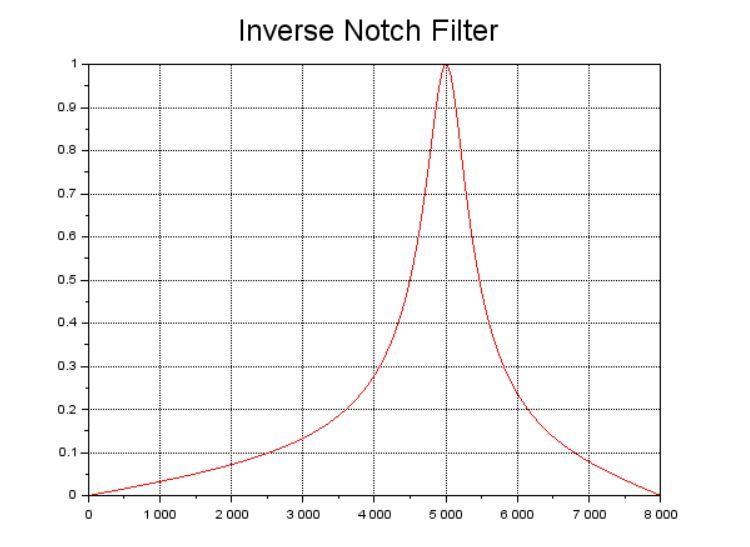
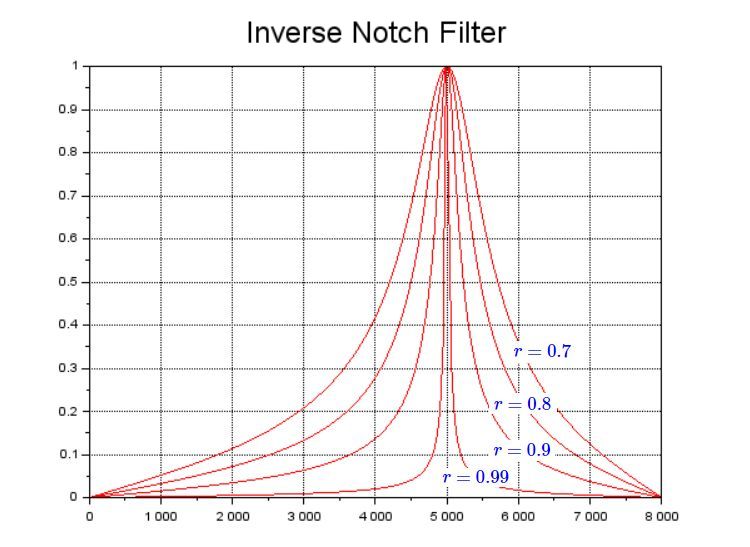
　上のグラフは、抽出周波数：5kHz、r：0.8での逆ノッチ・フィルターの周波数特性です。\(r\)は1未満の値を設定します。1に近いほど周波数特性は急峻になり、0に近いと緩やかになります。下のグラフは、同じ抽出周波数でr=0.99～0.7とした時にどのように変化するかをプロットしたものです。

　このように、デジタルフィルターはまるでマジックのように、わずかな計算式や係数の変更によって、周波数特性や動作を変化させることができるのには驚きです。そして、この逆ノッチ・フィルターはイコライザー作成の要になるフィルターです。

５．イコライザーの設計

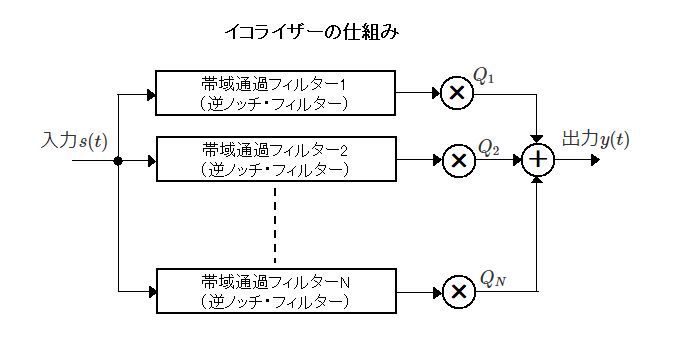
　イコライザーは、入力信号を特定の周波数帯域ごとに抽出して、それぞれの振幅を調整できるようにするものです。図のように、n個の逆ノッチ・フィルターを並列につないで、外部から変更することができる重み\(Q_n\)を掛けて振幅を調整し、それを合成することで実現します。
　設計段階では周波数帯域の設定方法などをいろいろ試してみましたが良い結果が得られず、先に参考文献に掲げた雑誌インターフェイス『音声信号処理』から、川村新さんの考え方をそのまま拝借させていただきました。
　次のように9個の逆ノッチ・フィルターを使用、つまり9バンドとし、各帯域の中心周波数を2倍ずつ変化させて、徐々に帯域幅を広げるようにしています。
　　　　\(32/64/128/256/512/1024/2048/4096/8192Hz\)
　すでに見たように、逆ノッチフィルターでは、抽出周波数から求められるフィルター係数\(a\)と\(r\)の値によって、その周波数帯域の周波数特性が決まります。
　下のグラフは、サンプリング周波数が\(24000Hz、r=0.8\)として、9つのバンドの周波数特性をプロットしたものです。これはイコライザーを構成する要素の例示であり、実際のイコライザーでは抽出周波数と帯域幅を指定して\(a\)と\(r\)を求めることになります。

６．イコライザーのコード

　コードを記述する前に、フィルター係数の計算方法を整理しておきましょう。
　まず逆ノッチ・フィルターの\(\ z\ \)領域伝達関数\(H(z)\)は次のように表すことができます。 \[ \ \ \ \ \ \ \ \ H(z) = \cfrac{(1-r)+(r-1)z^{-2}}{1+az^{-1}+rz^{-2}}\] 　ここまで、\(r\ \)はフィルター係数として\(r=0.8\)などの定数を充てていましたが、これは通過帯域幅\(K\)によって決まる係数として、次式で表わすことができます。各バンドの\(\ r\ \)は、ひとつ低域側のノッチ周波数の値を使って求めることにします。ここで\(F_s\)はサンプリング周波数です。
\[ \ \ \ \ \ \ \ \ r = \cfrac{1+cos(2{\pi}K/F_s)-sin(2{\pi}K/F_s)}{1+cos(2{\pi}K/F_s)+sin(2{\pi}K/F_s)}\] 　また\(\ a\)は、ゲインが1になるようにノッチフィルターを決めるフィルター係数で、次式で表されます。
　　　　\(a=-(1+r)cos\ {\omega}_N\)　　　ただし、\(\ {\omega}_N=2{\pi}F_c/F_s\)で、\(F_c\)はノッチ周波数

①データ領域

　配列は必要な要素数＋1で定義します。配列fcにはfc[1]から順次32～8192Hzのノッチ周波数を生成しますが、\(\ r\ \)の計算でひとつ低域側のノッチ周波数を使用するので、fc[0]に16Hzを設定しています。ステレオ処理を前提にしているので、音量調整には左右の音量係数を定義しています。これらの値はバンド別のアップ／ダウンキー操作で0.1ずつ増減できるようにします。

#define EQ_BANDS 9 // イコライザー・バンド数 // イコライザー用 double fc[EQ_BANDS+1] = {0}; // ノッチ周波数 double Ql[EQ_BANDS+1] = {0}; // 音量係数・左チャンネル double Qr[EQ_BANDS+1] = {0}; // 音量係数・右チャンネル double a[EQ_BANDS+1], r[EQ_BANDS+1]; // フィルター係数

②フィルター係数の計算

　アプリケーションの起動時に一度だけinitEqualizer関数を実行します。装置のサンプリング周波数を使ってフィルター係数を計算します。
　forの初期化式が1から始まりEQ_BANDSになるまでループすること、使用しないノッチ周波数fc[0]に初期値16.0を設定していること、帯域幅に低域側ノッチ周波数fc[i-1]*2を使っている点に注意してください。

/* initEqualizer : イコライザーの初期化処理 [引数] double Fs : サンプリング周波数 int level :　感度（0～9） */ void initEqualizer(double Fs) { double Ke; // 帯域幅 double w; fc[0] = 16.0; for (int i=1; i<=EQ_BANDS; i++) { Ke = fc[i-1]; // 帯域幅は低域側ノッチ周波数を使用 w = 2.0*M_PI*Ke/Fs; r[i] = (1 + cos(w) - sin(w)) / (1 + cos(w) + sin(w)); // 帯域幅を設定 fc[i]= fc[i-1] * 2; a[i] = -(1 + r[i]) * cos(2.0*M_PI*fc[i]/Fs); // フィルタ係数 } }

③イコライザー信号処理

　initEqualizer関数で算定されたフィルター係数とその時点の左右の音量係数を使って、入力音声の信号処理を行って出力バッファへ転送します。キー操作でバンド別の音量を調整をすると、音量係数配列QlまたはQrの値が変化してすぐに信号処理に反映され音量が変わります。コードの終わり部分のmute_swとvolumeは、次回の実装時にミュート機能と全体の音量調整機能を組み込むためのものです。
　ここで感度の調整値としてz=0.3としているのは、試行結果から適宜設定したものです。なお、遅延処理用のu0～u2はstatic変数としていることに注意してください。そうしないと、発振を伴うノイズが発生します（イコライザーの実装段階で問題が発生して足踏みしてしまいましたが、実はこれが原因でした）。

/* applyEqualizer : イコライザー信号処理関数 [引数] int frames : バッファのフレーム数 float *inptr : 入力バッファへのポインター float *outptr : 出力バッファへのポインター */ void applyEqualizer(int frames, float *inptr, float *outptr) { static double u0l[EQ_BANDS+1] = {0}; // u0～u2は静的変数でないとノイズが発生する static double u1l[EQ_BANDS+1] = {0}; static double u2l[EQ_BANDS+1] = {0}; static double u0r[EQ_BANDS+1] = {0}; static double u1r[EQ_BANDS+1] = {0}; static double u2r[EQ_BANDS+1] = {0}; double z = 0.3; //（感度の調整値） double xl, xr, sl, sr, yl, yr; for (int i=0; i<frames; i++) { sl = *inptr++; sr = *inptr++; yl = yr = 0; for(int j=1; j<=EQ_BANDS; j++) { u0l[j] = sl - a[j] * u1l[j] - r[j] * u2l[j]; // 逆ノッチフィルタの内部信号計算 u0r[j] = sr - a[j] * u1r[j] - r[j] * u2r[j]; xl = r[j] * u0l[j] + a[j] * u1l[j] + u2l[j]; // オールパスフィルタ出力計算 xr = r[j] * u0r[j] + a[j] * u1r[j] + u2r[j]; yl = yl + (Ql[j]*z) * (sl - xl)/2.0; // 逆ノッチ出力に感度をつけて加算 yr = yr + (Qr[j]*z) * (sr - xr)/2.0; u2l[j] = u1l[j]; u1l[j] = u0l[j]; // 信号遅延 u2r[j] = u1r[j]; u1r[j] = u0r[j]; } if (mute_sw == 0) { yl *= volume; yr *= volume; *outptr++ = (float)atan(yl / (M_PI/2.0)); // クリップ防止で出力バッファ転送 *outptr++ = (float)atan(yr / (M_PI/2.0)); } else { *outptr++ = mute_cst; *outptr++ = mute_cst; } } }

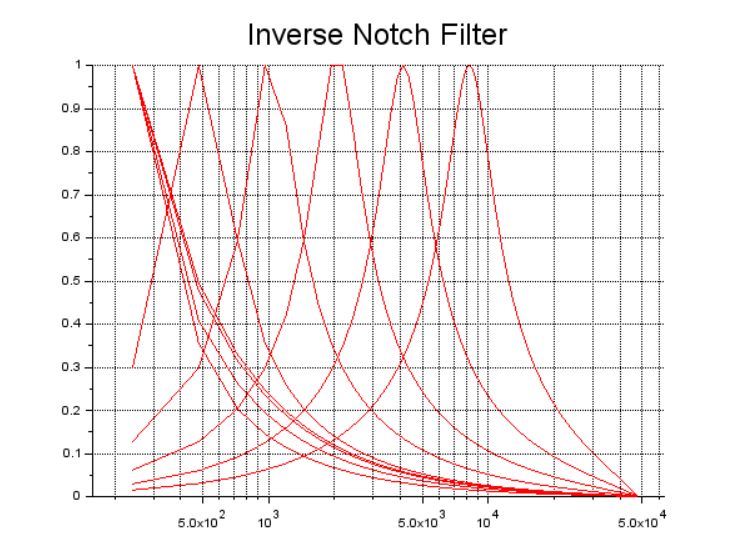
　以上のように、このイコライザーはノッチ周波数さえ設定すればフィルター係数が自動算定されて、これに従って信号処理が行われる仕組みになっています。下のグラフはイコライザーの周波数特性です。x軸は周波数の対数表示[Hz]、y軸はゲインで周波数成分を何倍にして出力するかを示しています。

　次回はいよいよイコライザーを実装します。また、ミュートや全体の音量調整機能なども盛り込む予定です。アプリケーションはしだいに複雑になりますが、もうひと踏ん張りです。お楽しみに！