１．音声とは何か

　まず、音声の仕組みと分析、音の特徴について整理しておきましょう。
○声の仕組み

　発生の仕組みを大まかに眺めると次のようになっています。
　　・肺から息が送られる
　　・声帯が振動する ---- 声がつくられる
　　・共鳴腔で声が増幅される ---- 共鳴で倍音が生まれる
　　・声道で共振周波数を決める ---- 音色が変化する（フィルターに相当する）
　　・口から音声波形が出る
　音声波形をデジタル信号に変換して、コンピューターで発生機構を近似する手法はソース・フィルターモデルと呼ばれます。この数理モデルによって、音声合成や音声分析が進められています。

○音声の分析

　音声を分析することで発話内容を認識することができます。
　　・声道の共振周波数をフォルマント周波数と呼びます。
　　・フォルマント周波数をグラフにすると、周波数が低い方から第1、第2、第3、･･･と振幅にピークができます。
　　・それぞれのピークは第1フォルマント(F1)、第2フォルマント(F2)、･･･と呼ばれます。
　　・F1とF2を、縦横に周波数を刻んだグラフにプロットすると、母音を識別することができます。
　これらの手法は進化して、音声認識や音声合成への応用が進められています。とりわけ線形予測符号化（LPC: linear predictive coding）技術は、明瞭な音声の合成や圧縮に大きく寄与。さらに確率モデルや統計手法を使ったアクセントの分析や、より自然な発生と音声変換への研究も進められています。

○物理的な音の特徴

　音の発生と特徴を簡単にまとめておきます。
　　・音は、太鼓やスピーカーのように物理的な振動によって発生します。音を発生させる物体を音源といいます。
　　・音源の振動で周りの空気が圧縮と膨張を繰り返し、空気の疎密が生じて音波が発生します。
　　・発生した音波は、縦波として媒体を伝わります。
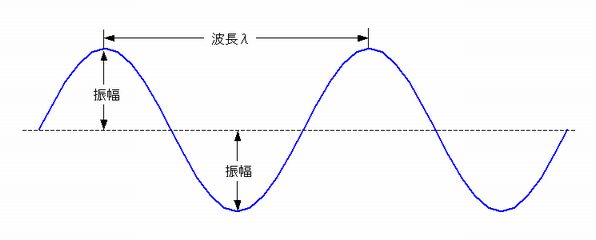
　　・疎密で伝達する縦波は視覚的にわかりにくいので、しばしば横波に変換して表示されます（下図のように）。
　　・空気中で音が伝わる速さは約340m、これは温度が15℃の時の速さです。
　　・次式で空気中での音速を求めることができます。ただし tは空気の温度（℃）です。
　　　　　\(v = 331.5 + 0.6t\)
　　・音は空気だけでなくヘリウムなどの気体や水などの液体、鉄のような固体も伝わります。
　　　水中では空気中の4～5倍の速さになります。しかし、真空中では音を伝える媒体がないので伝わりません。
　　・振動数、波長、音速には次の関係式が成り立ちます。
　　　　　\(v = f {\lambda}\)
　　　ただし、\(v\): 1秒間の音速[m/s]、\(f\): 1秒間の振動数[Hz]、\(\lambda\): 波長[m]、
　　・さらに、周期（波が1往復する時間）を T [s] とすると、
　　　　　\(f = \cfrac{1}{T} = \cfrac{v}{\lambda}\)

２．音の三要素

　物理的な音の要素として「音圧」「基本周波数」「周波数特性」があり、人はそれぞれを「音の大きさ」「音の高さ」「音色」として感じ取っています。

①音圧（音の大きさ）

　音圧は音波の振動する幅の大きさ（振幅）に比例します。
　波形データの最上部と最下部の絶対値が振幅になります。
　音の強さの国際単位は「Pa（パスカル）」ですが膨大な数値になるため、常用対数「dB（デシベル）」で表します。
　ちなみに「基準になる音」の\(x\)倍の\(dB\)値dbは次の式で求められます。
　　　　\(db = 20\log (x)\)
　日常生活での音の強さの目安は次のとおりです。

db	倍　率	日常の風景
0	1倍	人間の聴力限界（20μPa）
6	2倍	それより少し大きな音
10	3倍	静かな息
20	10倍	葉のカサカサ音
40	100倍	静かな図書館
60	1,000倍	通常の会話
80	10,000倍	電車、目覚まし時計
100	100,000倍	地下鉄の電車
120	1,000,000倍	ジェットエンジン

　また、最大の信号レベルと最小の信号レベルとの比をダイナミックレンジといいます。
　音楽CDに記録可能なダイナミックレンジはおよそ96dBです。
　　　その根拠は、CDは16ビットなので \(2^{16} = 65536\)、\(0\)を基準にする振幅の最大値は\(65535\)なので、
　　　　　　\(20\log(65535) = 96.33dB\)　となります。

②基本周波数（音の高さ）

　高さは音波が1秒間に振動する回数で決まります。波の間隔が狭ければ音は高く、広ければ低く感じます。
　音の高さは1秒間の振動回数を周波数「Hz（ヘルツ）」で表します。
　人間の可聴域は20Hz～20,000Hzとされています。

　ちなみに通常音階（十二平均律）の基準音として使用されるラの音（時報の最初の3つの音の音程）は440Hzです。1オクターブ上のラはその2倍の880Hzです。十二平均律はこの1オクターブを12等分した音階です。したがって、ある周波数を\(f\)とすると、その隣の音（半音上）は\(fr\)、二つ隣は\(fr^2\)････で、1オクターブ上は\(fr^{12}\)で表せます。そこで、次の等式が成り立ちます。
　　　　\(fr^{12} = 2f\)
　　　　\(r = ^{12}\sqrt{2}\)
　隣り合う音の周波数の比は2の12乗根となるわけです。
　基準音から\(n\)隣の音の周波数は次式で求めることができます（低い方は\(-n\)として）。
　　　　\(f = 440× r^n\)
　　　　　\(= 440×2^{n/{12}}\)

③周波数特性（音色）

　音波の形で決まり音響学では「周波数成分」とも呼びます。
　音色は大きくはエンベロープと倍音で変化します。エンベロープは音の立ち上がりから減衰して聞こえなくなるまでの音量の変化のパターンです。例えば安定して継続する管楽器の音と、比較的早く減衰するピアノやギターなどの音との違いです。
　また音には複数の周波数成分が含まれていますが、その中で最も周波数が低いものを「基音」と呼びます。基音より高い整数倍の周波数の「倍音」が、どんな構成でどのくらいの比率でできているかで音色の違いが生まれます。
　この倍音構成の比率を表したものを「スペクトラム」と呼びます。

　音圧と周波数の関係を時間変化でグラフにすると理解しやすくなります。下のグラフは周波数の異なる正弦波、400Hz、600Hz、1000Hzとその合成波をプロットしたものです。3つの正弦波の和が合成波に反映されていること、合成波の波長が構成波より長くなっていることなどがわかります。

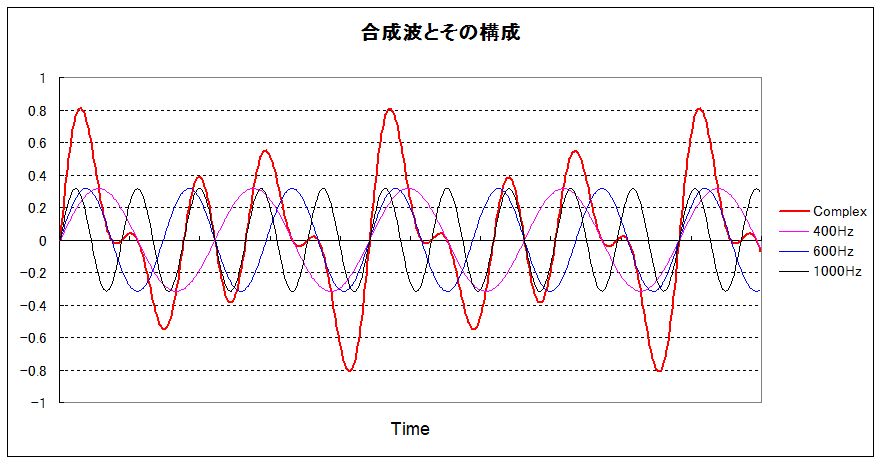
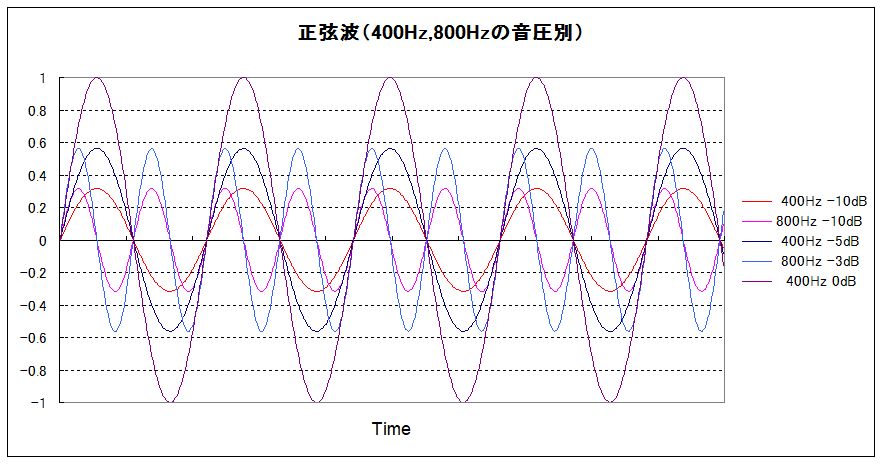
　次のグラフは、400Hzと800Hzの音圧が異なる正弦波をプロットしたものです。周波数が異なっても同じ音圧なら振幅は等しいこと、振幅の相対的な違いなどが明瞭です。

３．音波の性質と現象

　音波が媒体を伝わる中でさまざまな現象が起きます。これらを知って積極的に利用したり制御することが考えられます。
・うなり

　振動数が少しだけ違う音叉を鳴らすと、周期的に音が大きくなったり小さくなったりするのが聞こえます。
　うなりの回数 \(f'\)は、2つの音源の周波数\(f_1\)と\(f_2\)の差で求められます。
　　　　\(f = |f_1 - f_2|\)

・共鳴

　固有振動数が同じ二つの音源（例えば同じ音叉など）がある場合、片方の音源の振動が空気中を伝わってもうひとつの音源を振動させる現象です。

・反射

　山びこのように、音は山などで反射して返ってきます。音速と返ってくるまでの時間で、山までの距離を測ることができます。
　音波が壁などの物体にぶつかると、その壁自体が振動して再び音波が発生する。これによって生じるのが反響です。音源が停止しても音が響いて聞こえるのは残響と呼ばれます。

・ドップラー効果

　音源や観測者が動くと、音の高さ（振動数）が変化して聞こえる現象です。音源が移動するとき、その前方では音が進んだ距離から音源が進んだ距離が引かれるため音波の間隔が密になり、振動数が多くなって音が高くなります。逆の場合は音波の間隔が疎になり、振動数が小さくなるので音は低くなります。

・マスキング現象

　妨害音によって、ある音の最小可聴値が上昇する現象です。つまり、二つの音が重なっている時に片方の音がかき消されて聞こえなくなる現象です。

・モスキートーン

　17kHz(17000Hz)前後の高周波を指します。中高年層には聞こえにくい高い音です。聞こえる若者には不快に感じる（らしい）音です。

・ノイズキャンセリング

　ある音とまったく反対の波(逆位相)を発生することにより、その音の波を打ち消すものです。ノイズキャンセリングイヤフォンなどで使われている技術です。外部の余計な音をマイクで拾い、その音の逆位相を発生させて、聞きたい音、必要な音が聞こえる環境を作り出すことができます。

・ハース効果

　同じ音が複数の方向から同音量で発せられたときに、最も早く到達した音の音源の方向からすべてが聞こえているように感じてしまう現象です。

・カクテルパーティ効果

　周辺に雑音が多い中から特定の音を取り出す効果です。聞きたいことに神経を集中させることで雑音の中から聞きたい音が聞こえてくるもので、心理学的な領域であり未解明とされています。

４．音声信号処理とフーリエ級数

　今回の最後は、音声信号処理に欠かせないフーリエ変換のもとになるフーリエ級数の復習です。
　どんな複雑な波形でも、同じ周期をもつ波は正弦波の合成で表すことでができるとするものです。つまり、いろんな楽器の音色も三角関数の足し合わせで表現できるというわけです。このちょっと直感的には理解しにくい級数が、19世紀初めにフランスの数学者フーリエによって論文中に記載され議論が起きました。その後、この手法が様々な問題で使えることがわかり、今や、電気工学、振動解析、音響学、信号処理等々の幅広い分野で用いられています。そして、今後デジタルフィルターを理解するためにも避けて通れない重要な公式です。

　まず、\( 0 \leqq x \leqq 2\pi \)の範囲で定義された連続の関数\(f(x)\)を考えると、次の式が成り立つとしています。
\[ f(x) = c + \sum_{n=1}^{\infty}(a_n\cos(nx) + b_n\sin(nx)) \] 　これがフーリエ級数(Fourier series)です。
　波長が\(2\pi\)の\(\sin\)波と\(\cos\)波、その\(1/2\)の波長の\(\sin\)波と\(\cos\)波、\(1/3\)の波長の\(\sin\)波と\(\cos\)波、････というように、しだいに細かく上下するようになる波をいろんな振幅でどんどん積み重ねていくわけです。ここで\(c\)は\(f(x)\)の平均値なので次のように表されます。 \[ c = \cfrac{1}{2{\pi}}\int_{0}^{2{\pi}}f(x)dx \] 　係数\(a_n\)や\(b_n\)は次のようにして求めることができます。この式の成立過程は少々ややこしいので省略。興味がある方はこの後に紹介する『EMANの物理学・フーリエ級数の基本』を参照してください。 \[ a_n = \cfrac{1}{\pi}\int_{0}^{2{\pi}}f(x)\cos(nx)dx\\ b_n = \cfrac{1}{\pi}\int_{0}^{2{\pi}}f(x)\sin(nx)dx \] 　以上は\( 0 \leqq x \leqq 2\pi \)の範囲で考えていましたが、周期を自由に設定できるように拡張することができます。\(f(x)\)が周期\(T\)で繰り返す関数である場合、上記の式は以下のようになります。
\[ f(x) = \cfrac{a_0}{2} + \sum_{n=1}^{\infty}(a_n\cos\cfrac{2{\pi}nx}{T} + b_n\sin\cfrac{2{\pi}nx}{T}) \] 　ただし、 \[ a_n = \cfrac{2}{T}\int_{0}^{T}f(x)\cos\cfrac{2{\pi}nx}{T}dx\\ b_n = \cfrac{2}{T}\int_{0}^{T}f(x)\sin\cfrac{2{\pi}nx}{T}dx \] 　これでもなかなか納得がいかない人（私もそうなのですが）のために、実によくできたサイトを紹介しましょう。『EMANの物理学・フーリエ級数の基本』にアクセスして、まずは冒頭のウェブアプリ『フーリエ級数実演』を試してみてください。手書きで適当な波形を描いたら、それに向かってフーリエ級数がジワジワと迫ってくるのは圧巻です！

　さて、ここではフーリエ級数とはこんなものだという程度に理解しておけば大丈夫です。実際に使用するのは、これをベースにしたフーリエ変換や逆変換です。しかもコンピューターでは連続量（アナログデータ）ではなく離散量のデジタルデータを対象にすることから、離散フーリエ変換や逆離散フーリエ変換を使用することになります。

　次回はフーリエ変換について簡単に説明し、デジタルフィルター作成のための理論から設計へと進める予定です。
お楽しみに！