１．デジタルフィルターとは

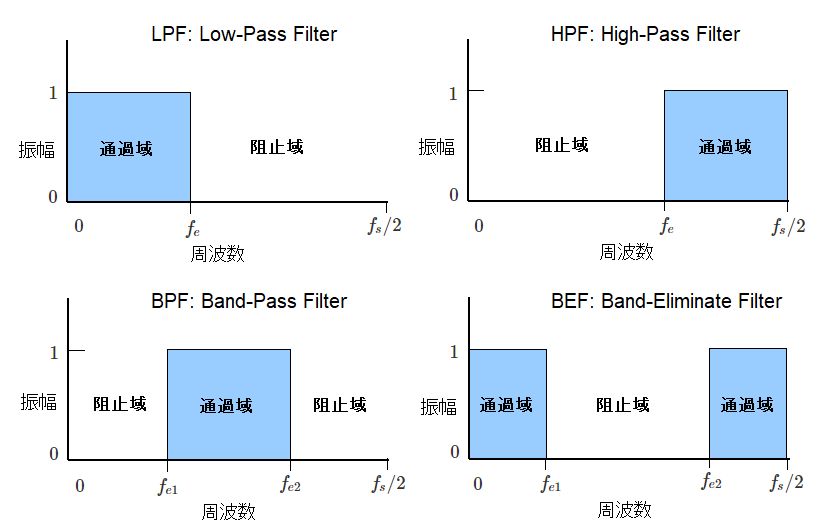
　フィルターは、特定の帯域の周波数成分だけを通過させる濾過器（ろかき）と言えます。下図に示すように、フィルターが通過させる帯域を「通過域」、フィルターが減衰させる帯域を「阻止域」と呼びます。
　基本的なフィルターは次の4種類に分類することができます。
　　　・低域の周波数成分を通過させる「低域通過フィルター（LPF: Low-Pass Filter）」
　　　・高域の周波数成分を通過させる「高域通過フィルター（HPF: High-Pass Filter）」
　　　・特定の周波数成分を通過させる「帯域通過フィルター（BPF: Band-Pass Filter）」
　　　・特定の周波数成分を減衰させる「帯域阻止フィルター（BEF: Band Eliminate Filter）」

　デジタルフィルターは、インパルス応答をどのように扱うかによって処理方式が分かれます。

○インパルス応答とは

　まず、フィルターの処理方式に関係するインパルス応答について簡単に整理しておきます。インパルス応答とは、インパルスと呼ばれる非常に短い信号を入力したときのシステムの出力のことです。
　例えばマイクの前で手をたたくと、オーディオ装置を通過した時間波形は最初が大きくて、時間経過と共に徐々に減衰していきます。この時間をできるだけ短くした時、手をたたいた音源で発生するのがインパルスで、オーディオ装置から出力される応答波形がインパルス応答です。
　インパルス応答つまり出力波形を分析することで、システムの特性（伝達関数）を把握することが可能になります。インパルス応答の長さをどうとらえるかによって、次のようにFIRフィルターとIIRフィルターに分かれます。

○FIR（Finite Impulse Response）フィルター

　インパルス応答が有限の長さで終わるとする方式です。
　FIRフィルターの主な特徴として次のことが挙げられます。
　　・フィルターの安定性が保証される。
　　・設計ツールを使うと比較的容易に実現できる。
　　・インパルス応答がその中心に関して偶対象となる場合、位相特性にひずみが生じない。
　　・計算量が膨大だが、ハードウェアの性能向上で問題なくなってきた。
　　・群遅延が発生する。

○IIR（Infinite Impulse Response）フィルター

　インパルス応答が無限であるとするものです。
　　・計算量が少ないため高速である。
　　・群遅延が発生しない。
　　・FIRフィルターに比べて低いフィルター次数で同じ特性を再現できる。
　　・メモリー消費が少なくハードウェアの負担を軽減できる。
　　・フィードバックを取り入れるので安定して動作させるための条件設計が重要。

　FIRとIIRの特徴を検討した結果、このプロジェクトではFIRで進めることにしました。以降の説明で特に断りがなければFIRフィルターと解釈してください。
　デジタルフィルターは、「乗算器」「加算器」「遅延器」という3種類の要素から構成されます。次に最も簡単な例として、\(b(0)\)を\(1\)、\(b(1)\)を\(-1\)にしたFIRフィルターを掲げます。これは、\(x(n)\)と\(x(n-1)\)の差を求めるフィルターで「微分フィルター」と呼ばれるものです。これがどのようにフィルターを構成するかは少し先の話になります。

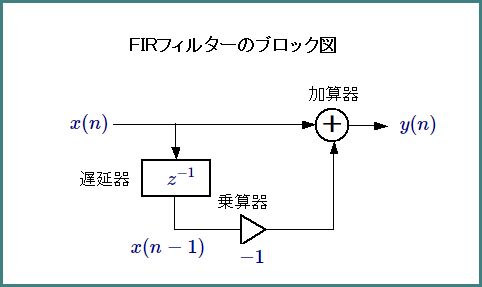
　このフィルターを式で表すと次のようになります。
　　　　　\(y(n) = x(n) - x(n-1)\)

２．フーリエ変換と周波数分析

　前回ではフーリエ級数について説明しましたが、この複雑な式が活躍するのはここからです。

①フーリエ変換

　複雑な波形がどのような正弦波の構成比率でできているかは、一見しただけではわかりません。周波数分析は、このような波形から周波数特性を割り出すための手法です。
　フーリエ級数は延々と同じ信号を繰り返す周期信号の周波数分析に有効ですが、音声信号などは周期信号になることはほとんどありません。そこで、無限長で非周期信号の\(x(t)\)から周波数特性を求める手法が必要になります。それが「フーリエ変換(FT: Fourier transform)」で可能になります。
　すべての時間で値をとるアナログ信号の周波数特性を調べるために考案されたもので、その逆変換である「逆フーリエ変換(IFT: inverse Fourier transform)」とともに次のように定義されています。 \[ X(f) = \int_{-\infty}^{\infty}x(t)e^{-j2{\pi}ft}dt\,　　　\,({-\infty}\le f\le{\infty})\tag{1-1} \] \[ x(t) = \int_{-\infty}^{\infty}X(f)e^{j2{\pi}ft}df\,　　　\,({-\infty}\le t\le{\infty})\tag{1-2} \] 　(1-1)が非周期的な時間関数\(x(t)\)からその周波数特性（スペクトル）\(X(f)\)を求めるフーリエ変換、(1-2)は逆に周波数スペクトル\(X(f)\)から元の時間信号\(x(t)\)を求める逆フーリエ変換です。

②離散フーリエ変換

　コンピューターではアナログ信号をそのまま扱うことができないため、アナログ信号を一定間隔（サンプリング周期）で分割してデジタル値に変換することはすでに述べたとおりです。
　先のフーリエ変換と逆フーリエ変換と同様に、離散化されたデジタル信号に対して変換するための「離散フーリエ変換(DTF: discrete Fourier transform)」と「逆離散フーリエ変換(IDFT: inverse discrete Fourier transform)」があります。これは式(1-1)と(1-2)に対して、次の関係にしたがって、\(t\)と\(f\)をそれぞれ\(0\)から\(N-1\)までの整数\(n\)と\(k\)に置き換えています。ここで、\(t_s\)は標本化周期、\(f_s\)は標本化周波数を表します。 \[ t = nt_s\,　　　\,\,\,(0\le n\le N-1)\\ f = \cfrac{kf_s}{N}\,　　　\,(0\le k\le N-1) \] 　そこで、離散フーリエ変換と逆離散フーリエ変換は次のように定義されます。 \[ X(k) = \sum_{n=0}^{N-1}x(n)e^{\frac{-j2{\pi}kn}{N}}\,　　　　\,(0\le k\le N-1)\tag{1-3} \] \[ x(n) = \cfrac{1}{N}\sum_{k=0}^{N-1}X(k)e^{\frac{j2{\pi}kn}{N}}\,　　　\,(0\le n\le N-1)\tag{1-4} \] 　(1-3)が離散フーリエ変換、(1-4)が逆離散フーリエ変換です。ここで、\(x(n)\)は時間\(n\)を変数とするデジタル信号の波形、\(X(k)\)は周波数\(k\)を変数とする\(x(n)\)の周波数特性を表しています。このようにNサンプルの波形が周期Nの周期信号であると仮定しているのがDTFの特徴です。
　ところで、AD変換のようにアナログ信号\(x(t)\)をデジタル信号\(x(n)\)に変換すると、\(X(f)\)は周期\(f_s\)の周期信号になります。こうしたデジタル信号に対するフーリエ変換とその逆変換は次のように定義されます。 \[ X(f) = \sum_{n=-\infty}^{x}x(n)e^{\frac{-j2{\pi}fn}{f_s}}\,　　　　\,(-f_s/2\le f\le f_s/2)\tag{1-5} \] \[ x(n) = \int_{-f_s/2}^{f_s/2}X(f)e^{\frac{j2{\pi}fn}{f_s}}df\,　　　\,(-\infty\le n\le\infty)\tag{1-6} \] 　この(1-6)式は、後述のフィルター設計において、周波数特性からフィルター係数を求めるために使用します。

　以上からわかるように、フーリエ変換は時間領域関数（波形）を周波数領域関数（スペクトラム）に変換する演算であるといえます。連続関数を対象としており、AD変換のサンプリングによって得られるようなデジタル値（波形データ）に対しては、離散フーリエ変換で時間領域から周波数領域への変換を行うのです。そして、それぞれ逆方向への変換もできるわけです

３．FIRフィルターの理論と特徴

①FIRフィルターの定義

　次図のようなFIRフィルターの構成をイメージして、FIRフィルターを定義してみましょう。

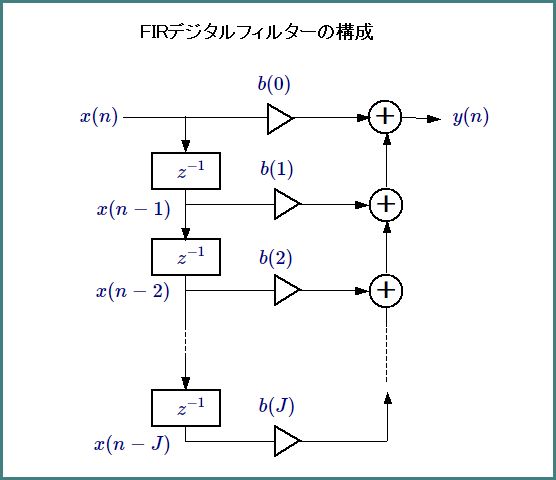　図のFIRフィルターは次式で定義されます。この式はコンボリューション（畳み込み）と呼ばれます。 \[ y(n) = \sum_{m=0}^{J}b(m)x(n - m)\tag{2-1} \] 　ここで、\(x(n)\)は入力信号、\(y(n)\)は出力信号、\(b(m)\)は乗算器のフィルター係数、\(J\)は遅延器の数です。
　\(m=0\)から開始するので、フィルター係数の数は\(J+1\)になります。

②Z変換とFIRフィルターの特徴

　デジタルフィルターの特性は「Z変換」と呼ばれる数学的な手法によって調べることができます。
　式(2-1)の\(x(n)\)と\(y(n)\)のZ変換は、それぞれ次のように定義されます。 \[ X(z) = \sum_{m=-\infty}^{\infty}x(n)z^{-n}\tag{2-2} \] \[ Y(z) = \sum_{m=-\infty}^{\infty}y(n)z^{-n}\tag{2-3} \] 　これらの定義に基づいて式(2-1)のZ変換を求めてみます。まず、式(2-1)を式(2-3)に代入してみます。 \[ Y(z) = \sum_{n=-\infty}^{\infty}\sum_{m=0}^{J}b(m)x(n-m)z^{-n}\tag{2-4} \] 　次にシグマ記号の順番を入れ替えると、 \[ Y(z) = \sum_{m=0}^{J}b(m)\sum_{n=-\infty}^{\infty}x(n-m)z^{-n}\tag{2-5} \] 　これは次のように書き換えることができます。 \[ Y(z) = \sum_{m=0}^{J}b(m)\sum_{n=-\infty}^{\infty}x(n-m)z^{-n+m}z^{-m}\tag{2-6} \] 　式(2-2)を考慮すると、式(2-6)は次のように書き換えられます。 \[ Y(z) = \sum_{m=0}^{J}b(m)X(z)z^{-m}\tag{2-7} \] 　ここで、\(b(m)\)は\((0\le m\le J)\)で値を持ち、その他は0になることを考慮すると、式(2-7)は次のように書くことができます。 \[ Y(z) = \sum_{m=-\infty}^{\infty}b(m)X(z)z^{-m}\tag{2-8} \] 　一方、\(b(m)\)のZ変換は次にように定義されます。 \[ B(z) = \sum_{m=-\infty}^{\infty}b(m)z^{-m}\tag{2-9} \] 　したがって、式(2-9)は次のように書き換えることができます。 \[ Y(z) = B(z)X(z)\tag{2-10} \] 　式(2-10)は、入力信号のZ変換\(X(z)\)とフィルター係数のZ変換\(B(z)\)をかけ合わせたものが出力信号のZ変換\(Y(z)\)になることを意味しています。これは、FIRフィルターの重要な特徴です。
　なお、入力信号を分母、出力信号を分子とした比を「伝達関数」と呼びます。伝達関数は、フィルターによって信号がどのように変化するかを定義したものになっており、FIRフィルターの伝達関数は次のように\(B(z)\)そのものになります。 \[ H(z) = \cfrac{Y(z)}{X(z)} = B(z)\tag{2-11} \] 　これらのZ変換は、デジタル信号に対するフーリエ変換と密接に関係しています。\(f\)を周波数とし、\(z\) →\(e^{j2{\pi}f}\)と置き換えると、式(2-2)、式(2-3)、式(2-9)はそれぞれ次のようになります。 \[ X(f) = \sum_{n=-\infty}^{\infty}x(n)e^{-j2{\pi}fn}\tag{2-12} \] \[ Y(f) = \sum_{n=-\infty}^{\infty}y(n)e^{-j2{\pi}fn}\tag{2-13} \] \[ B(f) = \sum_{m=-\infty}^{\infty}b(m)e^{-j2{\pi}fm}\tag{2-14} \] 　これらの式は、\(f(x)\)を1に正規化したデジタル信号に対するフーリエ変換に他なりません。
　以上を考慮すると、式(2-10)は次のように\(f\)を変数として表すことができます。 \[ Y(f) = B(f)X(f)\tag{2-15} \] 　式(2-15)は、入力信号の周波数特性\(X(f)\)とフィルター係数の周波数特性\(B(f)\)をかけ合わせたものが、出力信号\(Y(f)\)になることを意味しています。
　このように、入力信号の周波数特性をフィルターの周波数特性によって変化させることで、所望の周波数の出力信号を生成するのがFIRフィルターの仕組みであると言うことができます。
　また、式(2-1)と式(2-15)は表裏一体の関係にあり、それぞれ時間領域と周波数領域という2つの異なった視点からフィルタリングを眺めたものになっています。時間領域では畳み込み、周波数領域では乗算として定義されることがFIRフィルターの重要な特徴になっています。

４．FIRフィルターの設計

　いよいよフィルターの設計を始めることにしましょう。設計と言っても、アナログフィルターのようにコンデンサーや抵抗器をハンダ付けするのではなくて、ソフトウェア作成の前段階としてもうしばらく数式をいじり回すことになります。

①ローパスフィルターの設計

　通過域と阻止域の境を「エッジ周波数\(f_e\)」と定義すると、ローパスフィルターの理想的な周波数特性は、エッジ周波数より低域では1、それよりも高域では0になります。これは次のように定義することができます。 \[ B(f) = \begin{cases} 1 　　 (0 \le |f| \le f_e) \\ 0 　　 (f_e < |f| \le 1/2)\tag{3-1} \end{cases} \] 　この周波数特性からフィルター係数を求めるには、デジタル信号に対する逆フーリエ変換を利用します。式(3-1)を\(X(f)\)の代わりに式(1-6)に代入し、\(n\)を\(m\)に書き換え、\(f_s\)を1に正規化すると次のようになります。 \[ b(m) = \int_{-f_e}^{f_e}e^{j2{\pi}fm}df \,　　　\,({-\infty} \le m \le {\infty}) \tag{3-2} \] 　これを計算すると、理想的なローパスフィルターのフィルター係数は次のようになります。 \[ b(m) = 2f_e sinc (2{\pi}f_em) \,　　\,({-\infty} \le m \le {\infty})\tag{3-3} \] 　ただし、\(sinc(x)\)は「シンク関数」と呼ばれ、次のように定義されています。 \[ sinc(x) = \begin{cases} 1 　　　　　\,\, (x = 0) \\ \cfrac{\sin(x)}{x} 　　　 (otherwise) \end{cases}\tag{3-4} \] 　したがって、(\(x \ne 0\))における最終的なフィルター係数\(b(m)\)は次のようになります。 \[ b(m) = 2f_e \cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em} \,　　　\,({-\infty} \le m\le{\infty})\tag{3-5} \] 　以下、ローパスフィルターと同様にしてハイパスフィルター、バンドパスフィルター、バンドエリミネートフィルターの設計を行ってみましょう。

②ハイパスフィルターの設計

　ハイパスフィルターの周波数特性は次のように定義することができます。 \[ B(f) = \begin{cases} 0 　　 (0 \le |f| \le f_e) \\ 1 　　 (f_e < |f| \le 1/2)\tag{3-6} \end{cases} \] 　式(3-6)を式(1-6)に代入して\(b(m)\)を求めると \[ b(m) = sinc({\pi}m) - 2f_e sinc(2{\pi}f_em)\tag{3-7} \] 　(\(x \ne 0\))における最終的なフィルター係数\(b(m)\)は次のようになります。 \[ b(m) = \cfrac{sin(2{\pi}m)}{2{\pi}m} - 2f_e \cfrac{\sin(2{\pi}f_em)}{2{\pi}f_em} \,　　　\,({-\infty} \le m\le{\infty})\tag{3-8} \]

③バンドフィルターの設計

　バンドパスフィルターの周波数特性は次のように定義することができます。 \[ B(f) = \begin{cases} 0 　　 (0 \le |f| \le f_{e1}) \\ 1 　　 (f_{e1} < |f| \le f_{e2}) \\ 0 　　 (f_{e2} < |f| \le 1/2)\tag{3-9} \end{cases} \] 　式(3-9)を式(1-6)に代入して\(b(m)\)を求めると \[ b(m) = 2f_{e2}sinc(2{\pi}f_{e2}m) - 2f_{e1} sinc(2{\pi}f_{e1}m)\tag{3-10} \] 　(\(x \ne 0\))における最終的なフィルター係数\(b(m)\)は次のようになります。 \[ b(m) = 2f_{e2}\cfrac{sin(2{\pi}f_{e2}m)}{2{\pi}f_{e2}m} - 2f_{e1}\cfrac{\sin(2{\pi}f_{e1}m)}{2{\pi}f_{e1}m} \,　　　\,({-\infty} \le m\le{\infty})\tag{3-11} \]

④バンドエリミネートフィルターの設計

　バンドエリミネートフィルターの周波数特性は次のように定義することができます。 \[ B(f) = \begin{cases} 1 　　 (0 \le |f| \le f_{e1}) \\ 0 　　 (f_{e1} < |f| \le f_{e2}) \\ 1 　　 (f_{e2} < |f| \le 1/2)\tag{3-12} \end{cases} \] 　式(3-12)を式(1-6)に代入して\(b(m)\)を求めると \[ b(m) = sinc({\pi}m) - 2f_{e2}sinc(2{\pi}f_{e2}m) + 2f_{e1} sinc(2{\pi}f_{e1}m)\tag{3-13} \] 　(\(x \ne 0\))における最終的なフィルター係数\(b(m)\)は次のようになります。 \[ b(m) = \cfrac{sin({\pi}m)}{{\pi}m} - 2f_{e2}\cfrac{sin(2{\pi}f_{e2}m)}{2{\pi}f_{e2}m} + 2f_{e1}\cfrac{\sin(2{\pi}f_{e1}m)}{2{\pi}f_{e1}m} \,　　　\,({-\infty} \le m\le{\infty})\tag{3-14} \]

５．FIRフィルターと窓関数

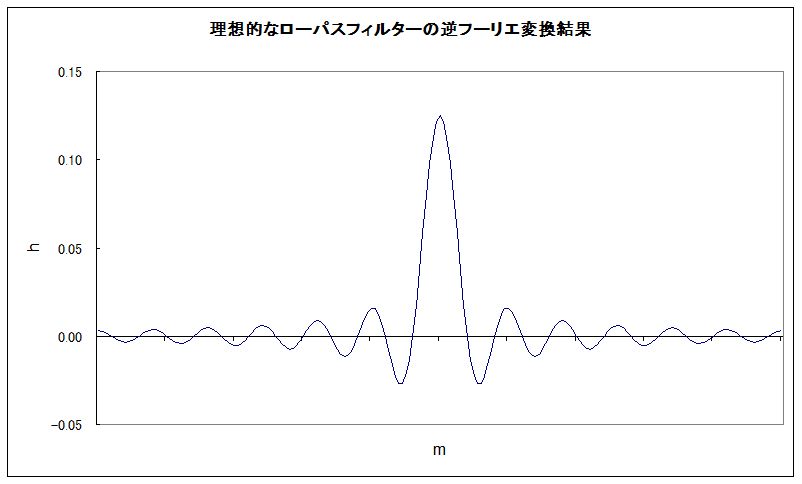
　以上で設計したFIRフィルターですが、このままではフィルターとしての性能はあまりよくありません。先の「離散フーリエ変換」で述べたように、DTFではNサンプルの波形が周期Nの周期信号であると仮定しています。いわば無限の時間関数から有限データを切り出して周期信号と見なしているわけで、Nの値によっては正弦波の不連続な部分で切り出して分析してしまい、本来存在しない周波数成分が現れて分析精度を落とすことになります。こうした問題を改善するために窓関数を利用します。以下に、理想的なローパスフィルターのフィルター係数と窓関数を適用した結果を示します。
　ついでながら、下のグラフは、次回に製作するローパスフィルターから201個のフィルター係数（-100～0～+100）を生成してプロットしたものです。ハニング窓関数と適用結果も同じ範囲で計算結果を求め、それぞれExcelでグラフ化しています。

　理想的なフィルターに見立てて十分に大きな幅でデータを切り出して、そのフィルター係数を求めてグラフ化すると、中央値が大きく、左右対称に急に値が落ち込んだ後はさざ波のように左右へ限りなく延びています。

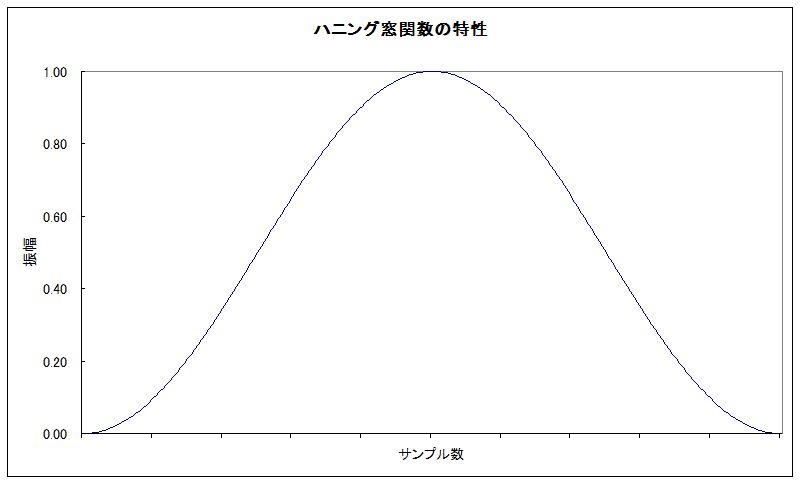
　窓関数にはハニング窓（ハン窓とも）やハミング窓などいくつか種類がありますが、ここでは最もよく利用されるハニング窓に絞って説明します。
　ハニング関数は次の式で表されます。 \[ w(x) = 0.5 - 0.5\cos 2{\pi}x \,　　　\,(0\le x\le1)\tag{4-1} \] ハニング窓関数は、グラフ化すると釣鐘型になるような係数を適用して、フィルター係数の両端を滑らかにゼロにします。

〔参考文献〕
　　　　青木直史(著)『サウンドプログラミング入門』 技術評論社(刊)
　　　　雑誌インターフェイス『音声信号処理』2016年6月号　CQ出版社(刊)
　　　　Web上の『小野測器・計測コラム』、その他たくさんの関連サイト／ページのお世話になりました。

　ふ～む、錆びた頭にはキツイ内容でした。しかし、いちばん不可思議だった時間領域と周波数領域の関係とか、それにフィルター係数や窓関数がどうかかわるかがわかったような･････。
　そして、ついにフィルター係数設計ツールとしても使える計算式を求めることができました。次回はこれらをC言語で関数化して、フィルター係数を生成してみましょう。余裕があれば、作成したフィルター係数をどのように適用して音声処理するかを考え、これも関数化したいと思っています。
　お楽しみに！